Recently I was asked by a client to build a scrolling isometric game. This series of blog posts will go in to some of my investigation into building an isometric game using Starling. Hopefully it sheds some light on the topic for others.

First off I needed to learn how isometric differs from traditional 2d games. Wikipedia had some great information:
http://en.wikipedia.org/wiki/2.5D
http://en.wikipedia.org/wiki/Isometric_projection

For the purposes of a game it looked like the most common implementation was a 2:1 projection. This keeps everything on square pixels. From here on out when I refer to “isometric” I am talking about this type of projection.

Tile images

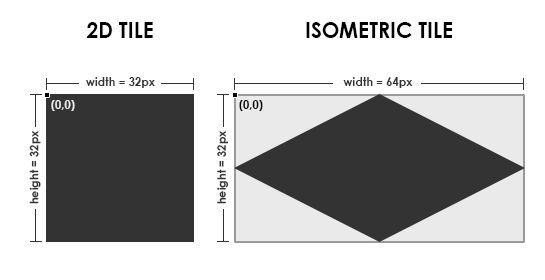
Using the 2:1 projection, isometric tile image sizes would be like 32×16, 64×32, 128×64 etc. See below how a 2d (32×32) tile looks in isometric (64×32). Note that the width of the image is doubled. I will keep the registration point in the top-left corner to keep consistent.

Tilemap

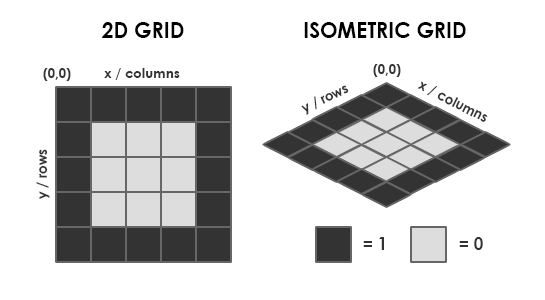
One easy way to represent a game map is with an Array. The code below represents a map with a 5×5 tile grid. A “1″ represents a wall and a “0″ for the floor or walkable tile.

 
var mapArray:Array = new Array(
	[1,1,1,1,1],
	[1,0,0,0,1],
	[1,0,0,0,1],
	[1,0,0,0,1],
	[1,1,1,1,1]
);
 

The image below shows how this map array is converted to a 2d tilemap and then isometric. Note the difference of the zero point (0,0). This now changes from top-left to top-middle of the tilemap.

Converting co-ordinates

Co-ordinates can be converted between 2d and isometric using the following formulas. You will be doing this a lot!

// convert 2d to isometric
xIso = (x2d - y2d);
yIso = (y2d + x2d)/2

// convert isometric to 2d
x2d = (2*yIso + xIso)/2;
y2d = (2*yIso - xIso)/2;

Or setup a helper function to convert either way:

// convert a 2d point to isometric
public static function convert2dToIsometric(pt2d:Point):Point
{
	var ptIso:Point = new Point();
	ptIso.x = (pt2d.x - pt2d.y);
	ptIso.y = (pt2d.x + pt2d.y)/2;
	return(ptIso);
}

// convert an isometric point to 2D
public static function convertIsometricTo2d(ptIso:Point):Point
{
	var pt2d:Point = new Point();
	pt2d.x = (2* ptIso.y + ptIso.x)/2;
	pt2d.y = (2* ptIso.y - ptIso.x)/2;
	return(pt2d);
}

Next

Once I understood how the co-ordinate systems differed it was time to get something going in Flash. I found a tutorial written by Tonypa which is actually a great series on games. These are all written in ActionScript 2 so I decided to try and port the isometric one to ActionScript 3 and Starling as my first step.

Go to Part II